Selasa, 18 Desember 2018

Matriks

Pengertian Matriks

Matriks adalah susunan beberapa bilangan atau huruf dalam bentuk persegi panjang, yang disusun menurut baris dan kolom serta dituliskan di antara tanda kurung.
Jenis-jenis matriks :
  1. Matriks baris: hanya terdiri dari satu baris (A_{1\times n})
  2. Matriks kolom: hanya terdiri dari satu kolom (A_{1\times m})
  3. Matriks nol: semua elemennya adalah nol
  4. Matriks persegi: jumlah baris dan kolomnya sama (A_{n\times n})
  5. Matriks diagonal: matriks persegi dimana elemen-elemen pada diagonal utamanya minimal terdapat sebuah elemen yang bukan nol, sedangkan semua elemen di luar diagonal utama adalah nol.
  6. Matriks skalar: matriks yang elemen-elemen diagonal utamanya sama, sedangkan di luar elemen diagonalnya sama dengan 0
  7. Matriks identitas: matriks diagonal dimana semua elemen pada diagonal utama adalah 1
  8. Matriks segitiga atas: matriks diagonal dimana elemen-elemen yang berada di atas diagonal utama minimal ada sebuah elemen yang bukan 0, sedangkan semua elemen di bawah diagonal utama adalah 0.
  9. Matriks segitiga bawah: matriks diagonal dimana elemen-elemen yang berada di bawah diagonal utama minimal ada sebuah elemen yang bukan 0, sedangkan semua elemen di atas diagonal utama adalah 0.
Matriks Transpose
Jika A = \begin{bmatrix} a_{1} a_{2} a_{3} ... a_{p} \\ b_{1} b_{2} b_{3} ... b_{p} \\ m_{1} m_{2} m_{3} ... m_{p} \end{bmatrix} maka A^{T}=\begin{bmatrix} a_{1} b_{1} \cdots m_{1} \\ a_{2} b_{2} \cdots m_{2} \\ a_{3} b_{3} \cdots m_{3} \\ \vdots \vdots \vdots \vdots \\ a_{p} b_{p} \cdots m_{p} \end{bmatrix}
Matriks A dan B dikatakan sama (A=B) jika dan hanya jika ordo kedua matriks sama dan elemen-elemen yang bersesuaian (seletak) juga sama.

Operasi-operasi Aljabar pada Matriks

  • Penjumlahan matriks Jika A = \begin{bmatrix} a_{1} a_{2} \\ a_{3} a_{4} \end{bmatrix} dan Jika B = \begin{bmatrix} b_{1} b_{2} \\ b_{3} b_{4} \end{bmatrix}, maka A+B = \begin{bmatrix} a_{1}+b_{1} a_{2}+b_{2} \\ a_{3}+b_{3} a_{4}+b_{4} \end{bmatrix}
  • Sifat Penjumlahan matriks
  1. Komutatif : A+B=B+A
  2. Assosiatif: (A+B)+C=A+(B+C)
  3. A+O=O+A=A, O adalah matriks nol.
  4. A+B=O, B disebut lawan atau negatif A, ditulis B=-A
  • Perkalian matriks dengan bilangan real Jika A = \begin{bmatrix} a_{1} a_{2} \\ a_{3} a_{4} \end{bmatrix} , maka kA=\begin{bmatrix} ka kb \\ kc kd \end{bmatrix}
  • Sifat-sifat Perkalian Matriks dengan Bilangan Real
  1. (q+r)A=qA+rA
  2. r(A+B)=rA+rB
  3. p(qA)=(pq)A
  • Perkalian matriks Jika A=\begin{bmatrix} a b \\ c d \end{bmatrix} dan Jika B=\begin{bmatrix} p q \\ r s \end{bmatrix} Maka AB=\begin{bmatrix} ap+br aq+bs \\ cp+dr cq+ds \end{bmatrix}
  • Sifat-sifat Perkalian matriks
  1. Assosiatif: (AB)C=A(BC)
  2. Distribusi kiri: A(B+C)=AB+AC
  3. Distribusi Kanan: (B+C)A=BA+CA

Invers dan determinan matriks Ordo 2×2

  • Jika, A dan B adalah matriks persegi yang berordo sama dam AB=BA=I, maka A disenut invers B, ditulis A=B^{-1}, dan B disebut invers A, ditulis B=A^{-1}
  • Determinan Matriks Ordo 2×2
Jika A=\begin{bmatrix} a b \\ c d \end{bmatrix}, maka det A = \begin{vmatrix} a b \\ c d \end{vmatrix} = ad-bc
dan det A^{-1}=\frac{1}{ad-bc}\begin{bmatrix} d -b \\ -c a \end{bmatrix},dengan 
Contoh soal menentukan invers matriks berordo 3 x 3
Tentukan invers matriks B yang diberikan pada persamaan di bawah.
    \[ \textrm{B} \; = \; \begin{bmatrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{bmatrix} \]
Pembahasan:
Menghitung nilai determinan B:
    \[ \left| \textrm{B} \right| \; = \; \left| \begin{matrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{matrix} \right| \]
    \[ \left| \textrm{B} \right| \; = \; 1 \cdot 3 \cdot 2 + 2 \cdot 1 \cdot 2 + 1 \cdot 3 \cdot 1 - 2 \cdot 3 \cdot 1 - 1 \cdot 1 \cdot 1 - 2 \cdot 3 \cdot 2 \]
    \[ \left| \textrm{B} \right| \; = \; 6 + 4 + 3 - 6 - 1 - 12 = - 6 \]

Menentukan Kofaktor:
Berikut ini adalah hasil perhitungan nilai-nilai kofaktor untuk matriks B. Silahkan lihat kembali bagaimana cara mendapatkan nilai kofaktor pada rumus yang telah dibahas di atas jika belum hafal rumusnya.
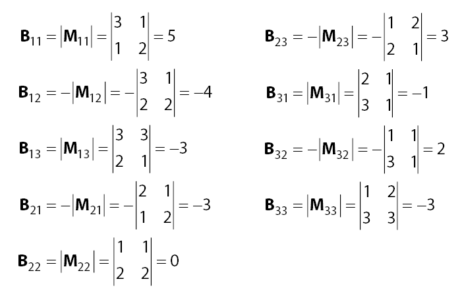
Matriks Kofaktor
Untuk menentukan invers B, kita membutuhkan matriks adjoin B. Sehingga, kita perlu menentukan matriks adjoin B terlebih dahulu.
  Menentukan Adjoin B:
Adjoin dari matriks B, sesuai dengan persamaan di atas akan diperoleh hasil seperti berikut.
Matriks Adjoin B
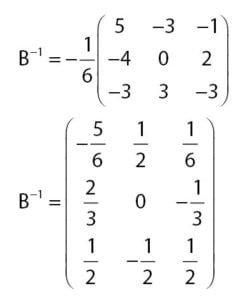
  Menentukan Invers Matriks B:
Persamaan umum untuk invers suatu matriks dinyatakan melalui persamaan di bawah.
    \[ B^{-1} \; = \; \frac{1}{det(B)} \cdot Adj(B) \]
Sehingga, diperoleh invers matriks B seperti hasil berikut.
Invers Matriks B

Det A \neq 0
Diposting oleh di

Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)