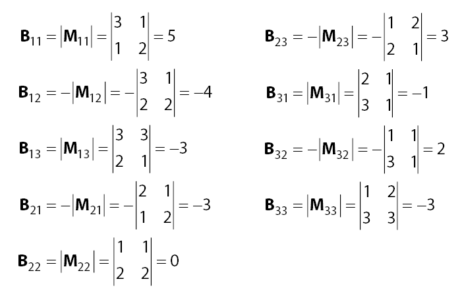Belajar MTK: 2018

Pangkat

Pengertian Bilangan Berpangkat

Dalam memahami pengertian bilangan berpangkat dapat dijelaskan melalui rumus berikut :

aⁿ = a x a x a x a x a ... x a sebanyak n

Aturan dasar pengoperasian bilangan berpangkat

Berikut 8 rumus dalam materi bilangan berpangkat yang admin rasa kalian harus memahami konsepnya karena akan sangat berguna untuk penyelesaian soal-soal matematika yang berhubungan dengan pangkat. yuk simak baik-baik.

Perkalian bilangan berpangkat yang bilangan pokoknya sama

Rumus : a^p x a^q = a^p+q
Contoh :
a. 2³ x 2² = 2³⁺² = 2⁵
b. 10^-1 x 10⁵ = 10^-1+5 = 10⁴
c. 5 x 5⁵ = 5¹⁺⁵ = 5⁶

Pembagian bilangan berpangkat yang bilangan pokoknya sama besar

Rumus : a^p : a^q = a^p-q

Contoh :
a. 2³ : 2² = 2^3-2 = 2¹ = 2
b. 10^-1 : 10⁵ = 10^-1-5 = 10^-6
c. 5 : 5⁵ = 5^1-5 = 5^-4

Pemangkatan bilangan berpangkat

Rumus : (a^p)^q = a^pxq
contoh :
a. (3⁴)² = 3^4x2 = 3⁸
b. (6^-2)³ = 6^-2x3 = 6^-6

Pemangkatan dari perkalian dua bilangan

Rumus : (a x b)^p = a^p x b^p
Contoh :
a. (2 x 5)² = 2² x 5² = 4 x 25 = 100
b. 2⁴ x 5⁴ = (2 x 5)⁴ = 10⁴ = 10000

Pemangkatan dari pembagian dua bilangan

Rumus : (a : b)^p = a^p : b^p
Contoh :
a. (2 : 5)² = 2² : 5² = 4 : 25 = 1/4
b. 2⁴ : 5⁴ = (2 : 5)⁴

SPLDV

Persamaan Dan Pertidaksamaan Linear Satu Variabel.

· Pernyataan adalah kalimat yang dapat ditentukan nilai kebenarannya (bernilai benar atau bernilai salah).

· Kalimat terbuka adalah kalimat yang memuat variabel dan belum diketahui nilai kebenarannya.

· Himpunan penyelesaian dari kalimat terbuka adalah himpunan semua pengganti dari variabel-variabel pada kalimat terbuka sehingga kalimat tersebut bernilai benar.

· Persamaan adalah kalimat terbuka yang dihubungkan oleh tanda sama dengan (=).

· Persamaan linear satu variabel adalah kalimat terbuka yang dihubungkan oleh tanda sama dengan (=) dan hanya mempunyai satu variabel berpangkat satu. Bentuk umum persamaan linear satu variabel adalah ax + b = 0.

· Penyelesaian persamaan linear adalah pengganti variabel x yang menyebabkan persamaan bernilai benar.

· Dua persamaan atau lebih dikatakan ekuivalen jika mempunyai himpunan penyelesaian yang sama dan dinotasikan dengan tanda .

· Suatu persamaan dapat dinyatakan ke dalam persamaan yang ekuivalen dengan cara:

a. Menambah atau mengurangi kedua ruas dengan bilangan yang sama;

b. Mengalikan atau membagi kedua ruas dengan bilangan yang sama.

· Bentuk Persamaan sebagai berikut :

· Suatu ketidaksamaan selalu ditandai dengan salah satu tanda hubung berikut.

a. untuk menyatakan kurang dari.

b. untuk menyatakan lebih dari.

c. untuk menyatakan tidak lebih dari atau kurang dari atau sama dengan.

d. untuk menyatakan tidak kurang dari atau lebih dari atau sama dengan.

· Pertidaksamaan adalah kalimat terbuka yang menyatakan hubungan ketidaksamaan .

· Untuk menentukan penyelesaian pertidaksamaan linear satu variabel, dapat dilakukan dalam dua cara sebagai berikut.

a. Mencari lebih dahulu penyelesaian persamaan yang diperoleh
dari pertidaksamaan dengan mengganti tanda ketidaksamaan
dengan tanda “=”.

b. Menyatakan ke dalam pertidaksamaan yang ekuivalen.

B. Menyelesaikan Sistem Persamaan Linear Dua Peubah / Variabel

Sistem persamaan linear dua variabel secara umum adalah sistem persamaan dalam bentuk :

a₁x + b₁y = k₁

a₂x + b₂y = k₂

sehingga persamaan linear tersebut dapat diselesaikan jika a1.b2 ¹ a2.b1 sehingga persamaan linear tersebut mempunyai titik potong di (x1,y1).

Untuk menyelesaikan / menentukan penyelesaian sistem persamaan linear dua variable dapat digunakan beberapa cara antara lain sebagai berikut :

1. Metode subsitusi

2. Metode eliminasi

3. Metode gabungan antara eliminasi dan subsitusi

1. Metode Subsitusi

Contoh :

Tentukan himpunan penyelesaian dari sistem persamaan linear 2x + 3y = 2.....(1)

x + y = 1 .....(2)

Jawab :

Dari persamaan x – y = 1 didapat x = 1 + y

2x + 3y = 2 → 2(y + 1) + 3y = 1 + y

x = y + 1 2y + 2 + 3y = 2

5y = 0

y = 0

y = 0 → x = 1 + y

x = 1 + 0

x = 1

jadi himpunan penyelesaiannya = {1, 0}

2. Metode Eliminasi

Dengan metode eliminasi tentukan himpunan penyelesaian dari

2x + 3y = 6

2x + y = -2

Jawab :

2x + 3y = 6

2x + y = -2 -

2y = 8

y = 4

2x + 3y = 6 │x 1 → 2x + 3y = 6

2x + y = -2 │x 3 → 6x + 3y = -6 -

-4x = 12

x = -3

Jadi penyelesaiannya x = -3, y = 4

HP = {-3, 4}

3. Metode gabungan eliminasi dan subsitusi

Dengan metode eliminasi dan subsitusi tentukan himpunan penyelesaian dari

3x + 4y = -1

x - y = 2

Jawab :

3x + 4y = -1 │x 1 → 3x + 4y = -1

x - y = 2 │x 3 → 3x - 3y = 6 -

7y = -7

y = -1

y = -1 → x – y = 2

x – (-1) = 2

x = 2 – 1

x = 1

Jadi himpunan penyelesaiannya ={1, -1}

C. Menyelesaikan Sistem Persamaan Linear Tiga Peubah / Variabel

1. Metode Subsitusi

Contoh :

Dengan metode subsitusi tentukan himpunan penyelesaian persamaan berikut !

2x + y - z = 3 ....(1)

x + y + z = 1 ....(2)

x – 2y – 3z = 4 ....(3)

Jawab :

Dari persamaan (2) x + y + z = 1 → x = 1 – y – z ....(4)

(4 dan 1) → 2x + y – z = 3

2(1 – y – z) + y – z = 3

2 – 2y – 2z + y – z = 3

-y – 3z = 1

y = -3z – 1 ....(5)

(3 dan 4) → x – 2y – 3z = 4

1 – y – z – 2y – 3z = 4

-3y – 4z = 3 ....(6)

(5 dan 6) → -3y – 4z = 3

-3 (-3z – 1) – 4z = 3

9z + 3 – 4z = 3

5z = 0

z = 0 ....(7)

untuk z = 0 disubsitusikan ke persamaan (5)

y = -3z – 1

y = -3(0) – 1

y = -1

untuk z = 0, y = -1, disubsitusikan ke persamaan (2)

x + y + z = 1

x – 1 + 0 = 1

x = 2

Jadi himpunan penyelesaiannya {(2, -1, 0)}

2. Metode eliminasi dan subsitusi atau gabungan

Contoh :

Dengan metode gabungan tentukan himpunan penyelesaian dari sistem persamaan berikut!

2x – y - 2z = -1 ....(1)

3x + 2y – z = 10 ....(2)

4x – y - 3z = - 3 ....(3)

Jawab

Dari persamaan (1) dan (3)

2x – y + 2z = -1 │ x 2 → 4x – 2y + 4z = -2

-4x – y – 3z = -3 │ x 1 → -4x – y – 3z = -3 +

-3y + z = -5 .... (4)

Dari persamaan (2) dan (3)

3x – 2y + z = 10 │ x 4 → 12x + 8y - 4z = 40

-4x – y – 3z = -3 │ x 3 → -12x – 3y – 9z = -9 +

5y – 13z = 31 .... (5)

Dari persamaan (4) dan (5)

-3y + z = -5 │ x 13 → -39y + 13z = -65

-3y(1) + z = -5 │ x 1 → 5y – 13z = 31 +

-34y = -34 .... (5)

y = 1

y = 1 disubsitusikan ke persamaan (4)

-3y + z = -5

-3(1) + z = -5

z = -5 + 3

z = -2

untuk y = 1, z = -2 disubsitusikan ke persamaan (1)

2x – y + 2z = -1

2x – 1 + 2(-2) = -1

2x – 5 = -1

2x = -1 + 5

2x = 4

x = 2

Jadi himpunan penyelesaiannya {(2, 1, -2)}

Matriks

Pengertian Matriks

Matriks adalah susunan beberapa bilangan atau huruf dalam bentuk persegi panjang, yang disusun menurut baris dan kolom serta dituliskan di antara tanda kurung.
Jenis-jenis matriks :

Matriks baris: hanya terdiri dari satu baris $(A_{1\times n})$
Matriks kolom: hanya terdiri dari satu kolom $(A_{1\times m})$
Matriks nol: semua elemennya adalah nol
Matriks persegi: jumlah baris dan kolomnya sama $(A_{n\times n})$
Matriks diagonal: matriks persegi dimana elemen-elemen pada diagonal utamanya minimal terdapat sebuah elemen yang bukan nol, sedangkan semua elemen di luar diagonal utama adalah nol.
Matriks skalar: matriks yang elemen-elemen diagonal utamanya sama, sedangkan di luar elemen diagonalnya sama dengan 0
Matriks identitas: matriks diagonal dimana semua elemen pada diagonal utama adalah 1
Matriks segitiga atas: matriks diagonal dimana elemen-elemen yang berada di atas diagonal utama minimal ada sebuah elemen yang bukan 0, sedangkan semua elemen di bawah diagonal utama adalah 0.
Matriks segitiga bawah: matriks diagonal dimana elemen-elemen yang berada di bawah diagonal utama minimal ada sebuah elemen yang bukan 0, sedangkan semua elemen di atas diagonal utama adalah 0.

Matriks Transpose
$Jika A = \begin{bmatrix} a_{1} a_{2} a_{3} ... a_{p} \\ b_{1} b_{2} b_{3} ... b_{p} \\ m_{1} m_{2} m_{3} ... m_{p} \end{bmatrix}$ maka $A^{T}=\begin{bmatrix} a_{1} b_{1} \cdots m_{1} \\ a_{2} b_{2} \cdots m_{2} \\ a_{3} b_{3} \cdots m_{3} \\ \vdots \vdots \vdots \vdots \\ a_{p} b_{p} \cdots m_{p} \end{bmatrix}$
Matriks A dan B dikatakan sama (A=B) jika dan hanya jika ordo kedua matriks sama dan elemen-elemen yang bersesuaian (seletak) juga sama.

Operasi-operasi Aljabar pada Matriks

Penjumlahan matriks $Jika A = \begin{bmatrix} a_{1} a_{2} \\ a_{3} a_{4} \end{bmatrix}$ dan $Jika B = \begin{bmatrix} b_{1} b_{2} \\ b_{3} b_{4} \end{bmatrix}$ , $maka A+B = \begin{bmatrix} a_{1}+b_{1} a_{2}+b_{2} \\ a_{3}+b_{3} a_{4}+b_{4} \end{bmatrix}$
Sifat Penjumlahan matriks

Komutatif : A+B=B+A
Assosiatif: (A+B)+C=A+(B+C)
A+O=O+A=A, O adalah matriks nol.
A+B=O, B disebut lawan atau negatif A, ditulis B=-A

Perkalian matriks dengan bilangan real $Jika A = \begin{bmatrix} a_{1} a_{2} \\ a_{3} a_{4} \end{bmatrix}$ , maka $kA=\begin{bmatrix} ka kb \\ kc kd \end{bmatrix}$
Sifat-sifat Perkalian Matriks dengan Bilangan Real

(q+r)A=qA+rA
r(A+B)=rA+rB
p(qA)=(pq)A

Perkalian matriks $Jika A=\begin{bmatrix} a b \\ c d \end{bmatrix}$ dan $Jika B=\begin{bmatrix} p q \\ r s \end{bmatrix}$ $Maka AB=\begin{bmatrix} ap+br aq+bs \\ cp+dr cq+ds \end{bmatrix}$
Sifat-sifat Perkalian matriks

Assosiatif: (AB)C=A(BC)
Distribusi kiri: A(B+C)=AB+AC
Distribusi Kanan: (B+C)A=BA+CA

Invers dan determinan matriks Ordo 2×2

Jika, A dan B adalah matriks persegi yang berordo sama dam AB=BA=I, maka A disenut invers B, ditulis $A=B^{-1}$ , dan B disebut invers A, ditulis $B=A^{-1}$
Determinan Matriks Ordo 2×2

$Jika A=\begin{bmatrix} a b \\ c d \end{bmatrix}$ , maka $det A = \begin{vmatrix} a b \\ c d \end{vmatrix}$ = ad-bc
dan $det A^{-1}=\frac{1}{ad-bc}\begin{bmatrix} d -b \\ -c a \end{bmatrix}$ ,dengan
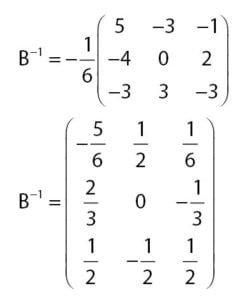
Contoh soal menentukan invers matriks berordo 3 x 3
Tentukan invers matriks B yang diberikan pada persamaan di bawah.

$\textrm{B} \; = \; \begin{bmatrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{bmatrix}$

Pembahasan:
Menghitung nilai determinan B:

$\left| \textrm{B} \right| \; = \; \left| \begin{matrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{matrix} \right|$

$\left| \textrm{B} \right| \; = \; 1 \cdot 3 \cdot 2 + 2 \cdot 1 \cdot 2 + 1 \cdot 3 \cdot 1 - 2 \cdot 3 \cdot 1 - 1 \cdot 1 \cdot 1 - 2 \cdot 3 \cdot 2$

$\left| \textrm{B} \right| \; = \; 6 + 4 + 3 - 6 - 1 - 12 = - 6$

Menentukan Kofaktor:
Berikut ini adalah hasil perhitungan nilai-nilai kofaktor untuk matriks B. Silahkan lihat kembali bagaimana cara mendapatkan nilai kofaktor pada rumus yang telah dibahas di atas jika belum hafal rumusnya.
Matriks Kofaktor

Untuk menentukan invers B, kita membutuhkan matriks adjoin B. Sehingga, kita perlu menentukan matriks adjoin B terlebih dahulu.
Menentukan Adjoin B:
Adjoin dari matriks B, sesuai dengan persamaan di atas akan diperoleh hasil seperti berikut.